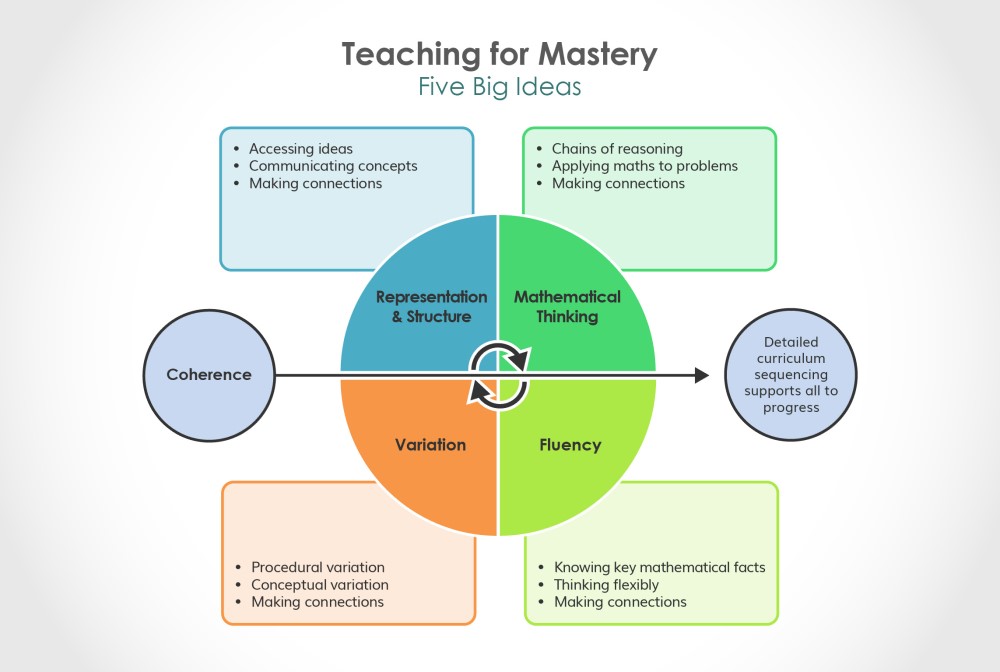
Five Big Ideas in Teaching for Mastery

The fundamental characteristics that underpin teaching for mastery in all school and college phases

Behind all NCETM and Maths Hubs work in the field of teaching for mastery are Five Big Ideas, all informed by research evidence and classroom experience. The diagram below [click/tap to enlarge] helps bind these ideas together

A true understanding of these ideas needs discussion with other teachers and an exploration of how the ideas are reflected in day-to-day maths teaching. On this page we share a flavour of what lies behind them.

For each of the Five Big Ideas - at both primary and secondary - there's an article exploring each idea in greater detail, accompanied by a short explainer video. You can find them all further down this page:

 

Coherence

Teaching is designed to enable a coherent learning progression through the curriculum, providing access for all pupils to develop a deep and connected understanding of mathematics that they can apply and communicate in a range of contexts.

Representation and Structure

Teachers carefully select representations of mathematics to expose mathematical structure. The intention is to support pupils in ‘seeing’ the mathematics, rather than using the representation as a tool to ‘do’ the mathematics. These representations become mental images that students can use to think about and discuss mathematics, supporting them to achieve a deep understanding of mathematical structures and connections.

Mathematical Thinking

Mathematical Thinking is central to how pupils learn mathematics and includes looking for patterns and relationships, making connections, conjecturing, reasoning, and generalising. Pupils should actively engage in mathematical thinking in all lessons, discussing and communicating their ideas using precise mathematical language.

Fluency

Efficient, accurate recall of key number facts and procedures is essential for fluency, freeing pupils’ minds to think deeply about concepts and problems, but fluency demands more than this. It requires pupils to have the flexibility to move between different contexts and representations of mathematics, to recognise relationships and make connections, to explain their ideas and to choose appropriate methods and strategies to solve problems.

Variation

The purpose of variation is to draw closer attention to a key feature of a mathematical concept or structure through varying some elements while keeping others constant. Through variation the teacher focuses thinking and discussion on the key feature in question.

Conceptual variation involves varying how a concept is represented to draw attention to critical features. Often more than one representation is required to look at the concept from different perspectives and gain comprehensive knowledge.

Procedural variation considers how the student will ‘proceed’ through a learning sequence. Purposeful changes are made in order that pupils’ attention is drawn to key features of the mathematics, scaffolding students’ thinking to enable them to reason logically and make connections.

The Five Big Ideas at Primary

Want to know more about the Five Big Ideas in the primary classroom? These features include a Q&A and a short explainer video:

The Five Big Ideas at Secondary

Want to know more about the Five Big Ideas in the secondary classroom? These features include a Q&A and a short explainer video:

The Five Big Ideas were first published by the NCETM in 2017.