Article

The Five Big Ideas at Secondary – Representation and Structure

What do representations look like in the secondary classroom?

09/05/2025

The Five Big Ideas at Secondary – Representation and Structure

Continuing our series on the Five Big Ideas at Secondary, we chat to Joe Cooper, Assistant Director for Secondary, about representation and structure. He explains how to select suitable representations, and how to tweak what you are already doing to get the best out of manipulatives.

What do we mean by Representation and Structure?

As teachers, we are always representing maths in some way – through language, images and symbols. This means that there is no getting away from representations! It is important that these representations are carefully planned and chosen to give students the best chance of learning the maths being taught.

The intention is to support students to ‘see’ the maths, rather than using the representation as a tool to ‘do’ the maths. Representations become mental images that students can use to think about and discuss maths, supporting them to achieve a deep understanding of mathematical structures and connections.

When we talk about representation and structure, we are usually talking about concrete or pictorial objects that in some way represent the maths being taught. They help us to understand the structure of maths behind them.

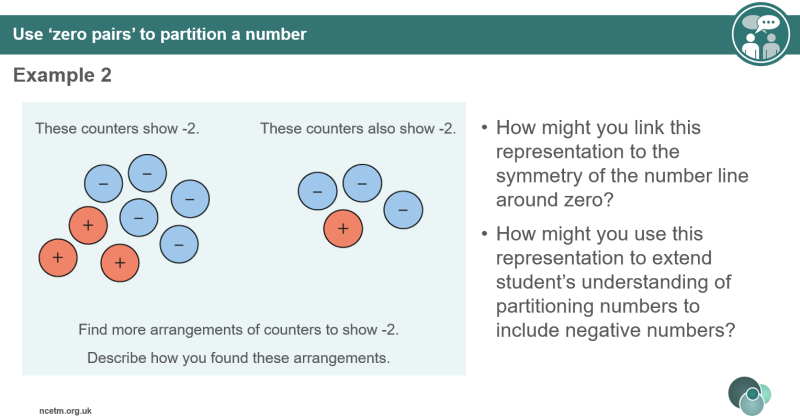
Representations can include diagrams or manipulatives that expose mathematical structures. For example, double sided counters can expose the structure of negative number arithmetic, with zero pairs giving a useful and clear representation of additive inverses that helps students to ‘see’ the underlying structure.

Click/tap image to enlarge

You’re probably already using representations regularly in your lessons. You might be using a bar model to expose the structure of the maths in a problem, or using algebra tiles to reveal the underpinning structure when manipulating algebra. You might be thinking about the moves between concrete (the physical tiles), pictorial (the area models these represent), and more abstract representations of the maths (the algebraic symbols).

Why are representations and structure in maths important for teachers?

Finding the right representation can open up a topic to a student. I remember the sudden clarity I felt when I saw ‘completing the square’ represented by an actual square rather than just algebraic manipulation. I’d been successful in manipulating the algebra, but this other representation suddenly made it clear why I was doing that.

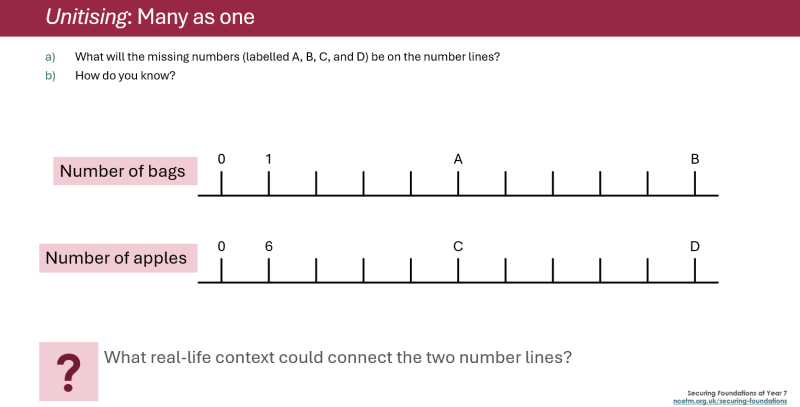
Some representations are integral to learning maths. Students won’t get far without an understanding of number lines, cartesian coordinates, algebraic graphs and the many other representations that are part of their mathematical education. Similarly, there are some representations that support learning from the start of KS1 to the end of KS5, and beyond. The area model, for example, supports students’ first steps in understanding numbers and multiplication, but can be equally well-used to explore quadratic equations and surds. This is because all these topics are connected to multiplication, which can be represented using areas.

Click/tap image to enlarge

How do representation and structure fit into the Five Big Ideas in Teaching for Mastery?

Careful use of representations and structure supports the underpinning principles explained in The Essence of Mathematics Teaching for Mastery. For example, representations provide access to the maths so that all students can learn and enjoy the subject. They also support students to make connections and provide a focus for discussions around reasoning. By providing a shared focus, representations can help students to engage with the maths and with each other.

When representations are well-planned in a department, they can be a vehicle for teachers to develop and work collaboratively. Curriculum design that includes carefully planned representations leads to students developing deep and sustained understanding of maths.

EXPLORE: The NCETM Checkpoints include a variety of representations to help expose mathematical structures

The most effective representations and mental models complement each other, and that isn’t a coincidence. Since double-sided counters represent a particular additive structure, they are used in the same way as small algebra tiles, because they are representing the same structure. This is just an example, but it shows the importance of using representations that convey the structure well, rather than ad-hoc representations. Carefully chosen representations work with each other, and provide a more coherent experience for learners.

Choosing to keep the representation the same but vary the nature of the examples might also draw students’ attention to different aspects of the maths. You might want to keep the same models but vary the question; for example, you might use a bar model in a ratio question, but then vary the missing information. You might choose to vary the model as you look at the same question to draw students’ attention to how the representation shows each part of the mathematical structure. What’s important is carefully considering what you want students to notice and how the representation supports that.

What are the challenges and benefits of using representations in lessons?

We should be careful of asking students to use unfamiliar representations to represent unfamiliar maths. One way to avoid this is to explicitly teach the representation and build up to using it with new mathematical concepts. When doing this, it’s important to let students know exactly what they are doing and why, otherwise they might think the maths has suddenly got too easy, or ignore the representation in favour of using a more familiar method.

Students might have experienced using manipulatives and diagrams only when the work is ‘too hard’, so may think that using them is an indication of failure. This couldn’t be further from the truth, so it’s important to deliberately plan for the use of manipulatives and diagrams in a coherent way and make sure that they aren’t just used to help correct a misconception or misunderstanding.

Representations aren’t just for younger students. Well-planned representations can support learning at all phases. There is a place for area models in upper KS4, just as much as at the start of KS3 (or even KS1!).

LEARN MORE: The guidance documents, Using mathematical representations at KS3, will help you discover the benefits and limitations of different representations.

It’s important to recognise that using a representation is different from teaching a method. Representations can lead to solutions to problems, but they are primarily about developing understanding rather than being the fastest way to solve a problem. Of course, students might choose to use a visual representation when they're solving a problem, but it's more likely they are going to move towards representing the structure using some formal maths, perhaps moving between representations.

What are your top tips for teachers?

Use them purposefully
Include representations thoughtfully, in a planned way and always in service to the learning.

Learn the representation and become comfortable with it
Just like students, teachers need to know the representation well. Explore what structures it reveals, how it connects to the maths, and where it might be most effective.

More is not better
There is no need to keep introducing new representations if students are not developing a deep understanding. Their use should be driven by student need, not by thinking each lesson needs a different manipulative.

Teach the representation
As well as considering the structures a representation will expose, make sure your students understand the important features of the representation and how it links to the maths.

Discuss the representation
Collaborate with your department and any support staff when planning, to make sure students across different classes have a coherent experience of representations.

Know when to stop
Representations are powerful, but their use is not limitless. If you find yourself bending the maths to fit the representation, it’s a sign it might not be the best tool for the job,

Plan your exit strategy
Support students to move beyond the concrete or pictorial stage when they’re ready—but let them revisit representations when it helps. Moving on does not mean you cannot return to a representation in the future.

To find out more about the Five Big Ideas, and to discover how your school could start using representations across the maths curriculum, contact your local Maths Hub or explore some of the professional development available.