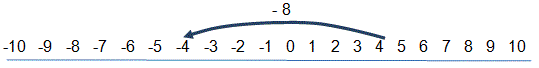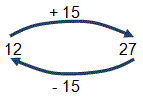• Developing a consistent effective approach to arithmetic and mathematical proficiency across a Learning Community to promote excellence in teaching and learning

  You might be interested in reading this Collaborative Teaching Project led by Barbara Nicolson Martin in 2012.The improvement agent and the maths subject leaders from 5 primary schools within the Braunton Learning Community plus the feeder secondary school researched the current methods of calculation used within their own schools, made comparisons and shared best practice. Together they formulated a joint approach to calculations and mathematical proficiency. They used current research including international comparisons and improved subject knowledge within their schools and encouraged mathematical flexibility across these phases of education leading to improved outcomes for children in: EYFS, KS1, KS2 and year 6 to year 7 transition.

• Mental Calculation Strategies for Addition And Subtraction: Thompson I, 1999

  In this article Ian Thompson discusses the difference between mental arithmetic and mental calculation and shares examples of how young children work out simple calculations. He draws conclusions on the most effective mental calculation strategies that our young children need to develop.

Activity set A

Use of concrete models and apparatus and helpful visual images are vital aspects of children’s mathematical activity – for all ages and all attainer groups. Knowing and using mental calculation strategies remain important in the National Curriculum. Use of manipulatives and mental strategies are practised and developed through a variety of short activities, for example:

• bridging through ten
• adding near multiples of 10 and adjusting

Give each child a 100 square. Ask them to put a finger on the number 3 and then give a series of instructions that involve the strategies above, for example: add 9 (add 10, subtract 1), add 13 (add 8 to get to 20 and then 5), take away 11 (subtract 10 and then another one). Activities similar to this, carried out regularly, will ensure that most children will remember and use them when appropriate.

You could also write four or five addition or subtraction calculations on the board for the children to represent in concrete, pictorial an abstract ways, for example:

Addition

• 35 + 36 (e.g. near doubles: double 35 and add 1)
• 36 + 49 (e.g. adding near multiples of 10: 36 + 50 – 1)
• 75 + 8 (e.g. bridging through 10: 75 + 5 + 3)
• 38 + 27 (e.g. partitioning: 30 + 20 = 50, 8 + 7 = 15, 50 + 15 = 65 or sequencing 38 + 20 + 7)

Subtraction

• 54 – 5 (e.g. bridging through 10: 54 – 4 – 1)
• 46 – 19 (e.g. subtracting near multiples of 10: 46 – 20 + 1)
• 50 – 25 (e.g. doubles: know two 25s make 50)
• 53 – 22 (e.g. sequencing: 53 – 20 – 2)

** Strategies given are examples, others can be used as efficiently.

You could give the children problems that they can answer using the strategy they think is best, which might include using practical apparatus, a number line, the bar model or a mental calculation strategy.

For example:

• Nathan had a collection of 46 coins. His friend gave him another 29. How many coins does he have now?
• Fran baked 97 cakes for the school cake sale. She sold 73. How many were left unsold?
• Ben had 25 football stickers. Bobby has 36. How many do they have in total? How many more stickers does Bobby have?

Activity set B

The children need to be able to recall and use addition and subtraction facts for all numbers to 20. They need to have plenty of practice in order to become fluent. Here are some examples of activities that can help:

• Write the number you wish the children to find facts for on the board, for example 18. Give the children a minute to write down as many facts as they can for addition and then another minute for subtraction facts. Encourage them to be systematic in their recording.
• Use a pendulum (three interlocking cubes on a piece of string), as it swings one way you call out a number to, say, 15 and as it swings the other way they call out the number pair that goes with it to make 15.
• Use a set of number cards to 20. Hold up one at a time. For each card you hold up the children write down the number that goes with it to make 20.

You can adapt these for any facts you wish to practice, including multiples of 5 and 10 to 100.

For practising number facts for 10, encourage the children to use their fingers. For example, ask them to show you the number of fingers needed to add to 8 to make 10, ask them to show you the number of fingers you need to take away from 10 to give four.

Activity set C

The children need to develop the understanding that addition is commutative (whichever way you add numbers the answers will always be the same). Provide plenty of practical experiences to show this:

• Give the children two different colours of counters and a simple addition to explore. Ask them to count out the correct number of coloured counters for one of those in the calculation and then the correct number of a different colour for the other number. Ask them to add one of the coloured counters to the other and then vice versa. What do they notice? The total is the same!
• You could then repeat the above with bead strings and base 10 apparatus.
• You could demonstrate this idea with the bar model:

The children could then explore this using a number line, for example:

The children need to develop the understanding that subtraction is not commutative. However, it is important that children don’t develop the misconception that they cannot take a larger number from a smaller one. This is only the case when dealing with concrete apparatus. Provide opportunities for the children to explore taking small numbers away on a number line. Give or show them a number line that begins with -10 and ends with 10. Ask them to put their finger on, for example, 4 and take away 8.

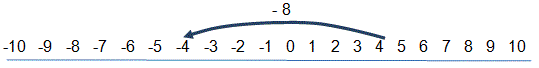
Some children develop the misconception that our number system begins with zero because this is how our number system is presented on many number lines. Most young children are aware of negative numbers in real life, for example winter temperatures. We need to capitalise on this from an early age to demonstrate that our numbers are replicated on the other side of zero with equivalent negative numbers.

Activity set D

In order to develop the understanding of the inverse relationship between addition and subtraction, the children initially need practical experiences. You could provide counters or similar apparatus. Ask the children to add two small quantities, for example 12 and 15. Once they have 27, ask them what they think they will have left if they take 15 away from the 27. Then ask them to check by taking 15 counters away leaving the other quantity.

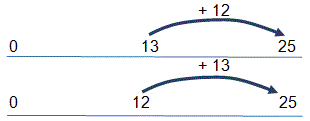
Inversion loops and the bar model are useful visual representations of inverse:

Inversion loops

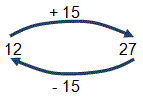
The bar model

You could give the children problems such as these to solve and then check using the inverse operation:

• Nafisat had 23 marbles. Her friend gave her 18 more. How many does she have now? The children add 23 and 18 to give 41. They then check by taking away 18 from 41 to give the original number.
• Adnaan had 36 sweets. He gave 21 to his friend. How many did he have left?

The children take 21 from 36 to give 15 and then check by adding 15 to 21 to give the original number.

Examples of what children should be able to do, in relation to each (boxed) Programme of Study statement

solve problems with addition and subtraction:

• using concrete objects and pictorial representations, including those involving numbers, quantities and measures
• applying their increasing knowledge of mental and written methods

add and subtract numbers using concrete objects, pictorial representations, and mentally, including:

• a two-digit number and ones
• a two-digit number and tens
• two two-digit numbers
• adding three one-digit numbers

• Use partitioning, counting strategies and knowledge of number bonds to add or subtract a one-digit number or a multiple of 10 to any two-digit number. To work out 86 – 50, for example, they might partition and calculate:

  86 – 50 = 80 + 6 – 50 = 80 – 50 + 6 = 30 + 6 = 36

• Similarly, to find the total number of people on a bus with 14 people on the top deck and 8 below, they might use:

  14 + 8 = 14 + 6 + 2 = 20 + 2 = 22

• Children add or subtract two-digit numbers using practical and informal methods and their knowledge of the relationships between operations. For example, they count back along a number line to find 64 – 25 or count up from 67 to find the answer to 94 – 67. They represent such calculations as number sentences. They calculate the value of an unknown in a number sentence such as ☐ ÷ 2 = 6 or 85 – ☐ = 29. They recognise, for example, that to answer 85 – ☐ = 29 they could use the related addition 29 + ☐ = 85

recall and use addition and subtraction facts to 20 fluently, and derive and use related facts up to 100

• Extend their knowledge and use of number facts, and use partitioning and number bonds to add and subtract numbers mentally to answer questions such as 60 – ☐ = 52 or 35 = 20 + ☐. They make jottings where appropriate to support their thinking.
• Answer problems such as:
  • Look at this number sentence: ☐ + ☐ = 20. What could the two missing numbers be? What else?
  • Can you tell me all the pairs of numbers that make 20?

show that addition of two numbers can be done in any order (commutative) and subtraction of one number from another cannot

• Understand that addition can be done in any order and use this to solve an addition by rearranging the numbers to simplify the operation. They need to understand that two numbers can be taken away from each other but that the answers will not be the same.

recognise and use the inverse relationship between addition and subtraction and use this to check calculations and missing number problems

• Check their addition and subtraction with a calculation that uses the inverse operation.
• Answer questions, such as:
  • Look at this number sentence: 74 – 13 = 61

    Write three more number sentences using these numbers. How do you know, without calculating, that they are correct?

  • What addition facts can you use to help you calculate these?

    12 – 5, 19 – 8

    Explain how the addition facts helped you.

  • I think of a number, I subtract 19 and the answer is 30. What is my number? How do you know?

Using resources to develop fluency and understanding

The video ‘Using resources to develop fluency’, demonstrates how Year 2 children can use straws and base ten equipment to help them develop a conceptual understanding of addition.