National Curriculum Resource Tool
Materials to support teachers and schools in embedding the National Curriculum
- National Curriculum Tool
- Year 4 - Measurement
Year 4 - Measurement
New Curriculum
- Convert between different units of measure [for example, kilometre to metre; hour to minute]
- measure and calculate the perimeter of a rectilinear figure (including squares) in centimetres and metres
- find the area of rectilinear shapes by counting squares
- estimate, compare and calculate different measures, including money in pounds and pence
- read, write and convert time between analogue and digital 12- and 24-hour clocks
- solve problems involving converting from hours to minutes; minutes to seconds; years to months; weeks to days.
Non-Statutory Guidance
Pupils build on their understanding of place value and decimal notation to record metric measures, including money.
They use multiplication to convert from larger to smaller units.
Perimeter can be expressed algebraically as 2(a + b) where a and b are the dimensions in the same unit.
They relate area to arrays and multiplication.
Links and Resources
Pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems. They should also apply their mathematical knowledge to science and other subjects.
– National Curriculum page x
Connections within Mathematics
Making connections to other topics within this year group
Number and place value Statutory requirements that are particularly relevant:
Pupils should be taught to:
- recognise the place value of each digit in a four-digit number (thousands, hundreds, tens, and ones)
- order and compare numbers beyond 1000
- identify, represent and estimate numbers using different representations
- round any number to the nearest 10, 100 or 1000
- solve number and practical problems that involve all of the above and with increasingly large positive numbers
When working on measurement and/or number and place value, there are opportunities to make connections between them, for example:
When converting between different units of measurement children need to know about the place value of digits. If converting, for example, 1.5km to metres they need to know that 1km is 1000m and that 0.5km is half of 1000m in order to give an answer of 1500m.
When solving problems involving measures or carrying out practical activities, it would be helpful to give the children opportunities to order different lengths, masses, capacities and volumes and also to round amounts to the nearest whole unit, ten, hundred etc. For example,you could ask the children to pick four cards and make a 4 digit number. They pretend their number represents grams and write them in as many different ways as they can, for example 4563 grams, 4kg 563g, 4.563kg. You could then ask them to round the grams to the nearest 10 (4560g), 100 (4600g) and 1000 (5000g). They could repeat this with metres and millilitres.
Addition and subtraction Statutory requirements (all are relevant):
Pupils should be taught to:
- add and subtract numbers with up to 4 digits using the formal written methods of columnar addition and subtraction where appropriate
- estimate and use inverse operations to check answers to a calculation
- solve addition and subtraction two-step problems in contexts, deciding which operations and methods to use and why.
When working on measurement and/or addition and subtraction, there are opportunities to make connections between them, for example:
When carrying out activities in measurement, provide opportunities for the children to solve problems that involve these types of calculation. For example:
- Freddie had a length of string which was 1m 75cm. He cut off two pieces, one 28cm and another 75cm and gave them to a friend. How much string did he have left?
- Hattie had 2l bottle of juice. She filled three glasses with 250ml of juice in each. How much juice was left in the bottle?
- Amy had saved £575. She bought laptop for £245.50 and a printer for £125. How much of her saving did she have left?
- Mandy left home at 10:30am. She arrived at the shopping centre 40 minutes later. What time did she get to the shopping centre?
- The film started at 17:45. Bobby was 35 minutes early. At what time did he arrive at the cinema?
They should be encouraged to decide which operations and methods to use and why.
Multiplication and division Statutory requirements that are particularly relevant:
Pupils should be taught to:
- recognise and use factor pairs and commutativity in mental calculations
- multiply two-digit and three-digit numbers by a one-digit number using formal written layout
When working on measurement and/or multiplication and division, there are opportunities to make connections between them, for example:
When converting from larger to smaller units the children should use multiplication, for example, 2km would be multiplied by 1000 to give 2000m. When converting from smaller to larger units division would be involved, for example, 200ml divided by 1000 would be 0.2l.
When looking at perimeter the children need to explore the algebraic formula of 2(a + b) where a and b are the dimensions in the same unit. This involves doubling or multiplying by two.
The notes and guidance suggests that the children study area through arrays of squares and discover for themselves that areas can be found by multiplying the number of rows by the number of columns which is the same as the length multiplied by the width.
Provide the children with opportunities to solve problems which involve multiplication and division. For example:
- Hammed wants to cover his back yard with grass. His back yard measures 12m by 10m. What area will he cover?
- Ahmed is going to sow grass seed in his garden. It is a rectangular measuring 8m by 4.5m. He needs to know the perimeter and area so he can buy the grass seed and bricks for the wall he wants to build around it. What are the perimeter and area of his garden?
Fractions Statutory requirements that are particularly relevant:
Pupils should be taught to:
- count up and down in hundredths; recognise that hundredths arise when dividing an object by one hundred and dividing tenths by ten.
- solve problems involving increasingly harder fractions to calculate quantities, and fractions to divide quantities, including non-unit fractions where the answer is a whole number
- add and subtract fractions with the same denominator
- recognise and write decimal equivalents of any number of tenths or hundredths
- recognise and write decimal equivalents to , ,
- find the effect of dividing a one- or two-digit number by 10 and 100, identifying the value of the digits in the answer as ones, tenths and hundredths
- round decimals with one decimal place to the nearest whole number
- compare numbers with the same number of decimal places up to two decimal places
- solve simple measure and money problems involving fractions and decimals to two decimal places.
When working on measurement and/or fractions there are opportunities to make connections between them, for example:
You could encourage the children to explore simple fractions of measurement such as ½, ¼ and ¾ of different numbers of centimetres, metres, kilometres, litres and kilograms. They could also do this for hours, perimeters and areas. This would reinforce the concept of finding a fraction by division.
Making connections to this topic in adjacent year groups
Year 3
- measure, compare, add and subtract: lengths (m/cm/mm); mass (kg/g); volume/capacity (l/ml)
- measure the perimeter of simple 2-D shapes
- add and subtract amounts of money to give change, using both £ and p in practical contexts
- tell and write the time from an analogue clock, including using Roman numerals from I to XII, and 12-hour and 24- hour clocks
- estimate and read time with increasing accuracy to the nearest minute; record and compare time in terms of seconds, minutes, hours and o’clock; use vocabulary such as a.m./p.m., morning, afternoon, noon and midnight
- know the number of seconds in a minute and the number of days in each month, year and leap year
- compare durations of events, for example to calculate the time taken by particular events or tasks
Non Statutory Guidance
Pupils continue to measure using the appropriate tools and units, progressing to using a wider range of measures, including comparing and using mixed units (e.g. 1 kg and 200g) and simple equivalents of mixed units (e.g. 5m = 500cm).
The comparison of measures should also include simple scaling by integers (e.g. a given quantity or measure is twice as long or five times as high) and this should connect to multiplication.
Pupils continue to become fluent in recognising the value of coins, by adding and subtracting amounts, including mixed units, and giving change using manageable amounts. They record £ and p separately. The decimal recording of money is introduced formally in year 4.
Pupils use both analogue and digital 12-hour clocks and record their times. In this way they become fluent in and prepared for using digital 24-hour clocks in year 4.
Year 5
- convert between different units of metric measure (e.g. kilometre and metre; centimetre and metre; centimetre and millimetre; gram and kilogram; litre and millilitre)
- understand and use equivalences between metric units and common imperial units such as inches, pounds and pints
- measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres
- calculate and compare the area of squares and rectangles including using standard units, square centimetres (cm2) and square metres (m2) and estimate the area of irregular shapes
- estimate volume (e.g. using 1 cm3 blocks to build cubes and cuboids) and capacity (e.g. using water)
- solve problems involving converting between units of time
- use all four operations to solve problems involving measure (e.g. length, mass, volume, money) using decimal notation including scaling.
Non Statutory Guidance
Pupils use their knowledge of place value and multiplication and division to convert between standard units.
Pupils calculate the perimeter of rectangles and related composite shapes, including using the relations of perimeter or area to find unknown lengths. Missing measures questions such as these can be expressed algebraically 4 + 2b = 20 for a rectangle of sides 2 cm and b cm and perimeter of 20cm.
They calculate the area from scale drawings using given measurements.
Pupils use all four operations in problems involving time and money, including conversions (e.g. days to weeks, leaving the answer as weeks and days).
Cross-curricular and real life connections
Learners will encounter measurement in:
Within the science curriculum there are opportunities to connect with measurement, for example, one of the requirements for states of matter is that the children should be taught to identify the part played by evaporation and condensation in the water cycle and associate the rate of evaporation with temperature. This could involve measuring temperatures using a thermometer and tracking the changes over, for example, a morning. The children record the temperature every 40 minutes making a note of the time in 24 hour digital format.
Within the design and technology curriculum there will be plenty of opportunities for accurate measuring, particularly of length using different units in the designing and making stages.
Within the cooking and nutrition curriculum the children should be taught to prepare and cook a variety of predominantly savoury dishes using a range of cooking techniques. As they work on these practically they will need to measure mass and volume. You could provide them with recipes and ask them to scale them up or down for different numbers of people and then to measure out the correct ingredients. If they require cooking time, the children could make up timetables to show preparation, cooking and clearing up times using 12 or 24 hour digital formats.
In real life, measurement is something that we frequently do without even thinking about it. You could ask the children to think about what they have done from waking up in the morning that has involved measuring. They might think of ideas to do with length (distance walking into school), mass (weight of their back pack),capacity and volume (filling their flask with juice), time (leaving home to get to school on time).
- Williams, R. F. (2004), Meaning from a Clock: Material Artefacts and Conceptual Blending in Time-Telling Instruction
Dr Williams investigates the relationship between material structures and conceptual operations in the everyday activity of time-telling. Telling time is crucial to modern life but cannot be mastered without instruction. He aims to answer these questions:
- Where did our time-telling artefacts and practices come from?
- How do we read the time from an analogue clock face?
- How does each new generation learn to perform this activity?
- Horner V., (2005) Charlotte’s Clock from the May/June 2005 issue of 'Special Children'
This article explains how Vicki Horner had to find a new way of teaching her daughter how to tell the time. It is a way that teachers might find helpful
- Douglas H. Clements D. H.(1999), Teaching length measurement: Research Challenges.
This article explores the difficult nature of teaching and learning the concept of length, suggesting the difficulty might be due to the fact that it bridges both spatial awareness and real numbers. It also challenges the conventional progression of skills related to the teaching of length.
- McLeod S. (2010) Concrete Operational Stage (Simply Psychology)
This article explores the work of Piaget. Children often believe that the amount of liquid has changed when a set amount has been poured from one container to another of a different size. Piaget would argue that children are not able to understand this notion of conservation until they have reached 7 to 11 years of age.
| Programme of Study statements | Activities | |||
| A | B | C | D | |
| convert between different units of measure (e.g. kilometre to metre; hour to minute) | ||||
| measure and calculate the perimeter of a rectilinear figure (including squares) in centimetres and metres | ||||
| find the area of rectilinear shapes by counting squares | ||||
| estimate, compare and calculate different measures, including money in pounds and pence | ||||
| read, write and convert time between analogue and digital 12 and 24-hour clocks | ||||
| solve problems involving converting from hours to minutes; minutes to seconds; years to months; weeks to days | ||||
Activity set A
(i) You could copy these units onto card and cut them out to give to the children to match:
| 1kg 750g | 1l 224ml | 1km 500m | 2550g | 1245cm | 10050l |
| 1m 10cm | 25mm | 6kg 75g | 1.75kg | 1.224l | 12m 45cm |
| 103mm | 1500m | 2.65l | 2l 650ml | 2cm 5mm | 1750g |
| 2.55kg | 6.075kg | 10l 50ml | 6075g | 12l 450ml | 2l 650ml |
| 12450ml | 10.05l | 12.45m | 1.45l | 1.5km | 1.10cm |
| 2.5cm | 10.3cm | 1.1m | 1224ml | 2kg 500g | 10cm 3mm |
(ii) You could ask the children to work in groups of 4 or 5. Each child will need a piece of modelling clay or plasticine. Time them for 30 seconds while they roll their plasticine into the longest ‘worm’ that they can. After 30 seconds, they place their ‘worms’ in order from shortest to longest. They estimate the shortest worm and write their estimate down in both centimetres and millimetres, e.g. 54mm, 5.4cm. Then they measure it, write that down in centimetres and millimetres and then work out the difference between their estimate and the actual measurement. They use this measurement to estimate the length of the next worm. Then measure it and so on for all the ‘worms’.
Activity set B
You could give the children problems similar to these:
- Sophie would like to build a rectangular patio in her garden. She wants the area of her patio to be 24m2.
What to do:
- Think about the possible sizes that Sophie’s patio could be. Write these down.
- Draw some designs using these sizes.
- Draw these to a scale of 1cm = 1m.
- Use another piece of paper if you need more room.
- Measure accurately using your ruler. Label the measurements
- Once you have drawn your rectangles, check to make sure the areas are correct.
- Work out the perimeters of each shape using the formula 2(a x b).
- Sam has been given a large area of land. He would like to build a stable for his horse on part of it. He wants it to be rectangular with a perimeter of 50m.
What to do:
- On paper work out some of the possible areas for Sam’s stable. Write them down.
- On a piece of squared paper, sketch some designs using these sizes.
- Use the scale of 1cm = 1m. Remember to label them.
- Once you have drawn your rectangles, check to make sure the perimeters are correct.
- Work out the areas of each shape in the most efficient way you can.
You might like to give the children the ‘Area and Perimeter’ problem from Nrich which asks them to create shapes with different areas and perimeters.
Or this one: ‘Numerically Equal’ which asks the children to draw a square with the same numerical values for its perimeter and its area
Activity set C
(Firstly, ensure that you, yourself, are very clear about the difference between volume and capacity. It is important that you are able to explain clearly and model use of the language correctly.)
You could ask the children to work in groups of four and carry out this activity
- Collect 4 different containers from around the classroom. They all need to look different.
- As a group estimate the capacity of one of your containers.
- Write your estimate on paper in litres and also millilitres.
- Measure the amount you estimated into a measuring jug and see if it fills the container.
- If your estimate was not correct. Find out how the actual capacity of the container. Add this information to the table.
- Repeat this for the other 3 containers.
You could give groups of children some sand, weighing scales, a book and some plastic bags and ask them to try out this activity:
- Sara says: I can make three different masses using bags of sand. These will help me estimate the mass of a dictionary.
- What do you think?
- How are you going to find out?
- Do you agree with Sara?
You could ask the children problems within the context of money. Ask them to estimate their answers first by rounding the money to the nearest pound. For example:
- Leona saved £50. She wants to buy a music player for £23.48. She also wants to download music from the internet. This will cost £9.67. Does she have enough money left to buy some headphones at £8.96?
- Paul and Lisa were making a list of food they would like to buy for their party. This is their list so far with the prices for the amounts they need:
Food Price French Sticks £4.45 Doughnuts £9.99 Tubs of ice cream £15.25 Pizzas £42.80 Samosas £4.50 Cheese sticks £10.75 They have £75. How much more money do they need to buy everything on this list?
- Billy had 10 coins. They totalled £4.50. What coins could they be? How many possibilities can you find?
Activity set D
You could give the children problems similar to these and ask them to solve them using a number line:
- Cherri went strawberry picking. She began at 10:20 and was picking strawberries for 2 hours 45 minutes. When did she finish?
- Adnan spent 1 hour 55 minutes at the gym. She left at 16:30. When did she get there?
- The twins went to the beach. They arrived at 11:50 and left at 17:15. How long were they at the beach for?
- Zeina and Mona left for school at 07:15. They spent the day working hard. They got home at 17:05. How long were they away from home?
- Brent and Chris were gardening. They started at 13:25. Brent finished at 15:55. Chris carried on for another hour and ten minutes. For how long was Chris gardening?
Next, ask the children to make up and solve some problems of their own.
You could give the children opportunities use their mental calculation skills of, for example, addition, subtraction, multiplication, doubling and halving to deduce new information about units of time:
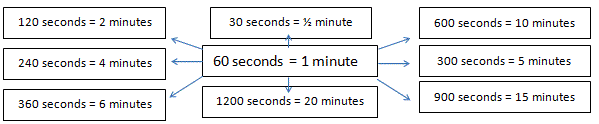
You could repeat this for days in different numbers of weeks, months in different numbers of years and so on.
Examples of what children should be able to do, in relation to each (boxed) Programme of Study statement
Convert between different units of measure [for example, kilometre to metre; hour to minute]
- Learn the relationships between familiar units of measurement. They learn that kilo means one thousand to help them remember that there are 1000 grams in 1 kilogram and 1000 metres in 1 kilometre. They respond to questions such as: A bag of flour weighs 2 kg. How many grams is this? They suggest suitable units to measure length, weight and capacity; for example, they suggest a metric unit to measure the length of their book, the weight of a baby, the capacity of a mug. They suggest things that you would measure in kilometres, metres, litres, kilograms, etc.
- Record lengths using decimal notation, for example recording 5 m 62 cm as 5.62 m, or 1 m 60 cm as 1.6 m. They identify the whole-number, tenths and hundredths parts of numbers presented in decimal notation and relate the whole number, tenths and hundredths parts to metres and centimetres in length.
measure and calculate the perimeter of a rectilinear figure (including squares) in centimetres and metres
- Measure the edges of a rectangle and then combine these measurements. They realise that by doing this they are calculating its perimeter. Given the perimeter of a rectangle they investigate what the lengths of its sides could be. They work out the perimeter of irregular shapes drawn on a centimetre square grid, e.g. using the ITP ‘Area’.
Find the area of rectilinear shapes by counting squares
- For example, they draw irregular shapes on centimetre square grids, and compare their areas and perimeters.
estimate, compare and calculate different measures, including money in pounds and pence
Draw on their calculation strategies to solve one- and two-step word problems, including those involving money and measures. They use rounding to estimate the solution, choose an appropriate method of calculation (mental, mental with jottings, written method) and then check to see whether their answer seems sensible. They throw a beanbag three times and find the difference between their longest and shortest throws. After measuring their height, they work out how much taller they would have to grow to be the same height as their teacher. They solve problems such as:
- Dad bought three tins of paint at £5.68 each. How much change does he get from £20?
- A family sets off to drive 524 miles. After 267 miles, how much further do they still have to go?
- Tins of dog food cost 42p. They are put into packs of 10. How much does one pack of dog food cost? 10 packs?
- A can of soup holds 400 ml. How much do 5 cans hold? Each serving is 200 ml. How many cans would I need for servings for 15 people?
- I spent £4.63, £3.72 and 86p. How much did I spend altogether?
- A string is 6.5 metres long. I cut off 70 cm pieces to tie up some balloons. How many pieces can I cut from the string?
- A jug holds 2 litres. A glass holds 250 ml. How many glasses will the jug fill?
- Dean saves the same amount of money each month. He saves £149.40 in a year. How much money does he save each month?
read, write and convert time between analogue and digital 12- and 24-hour clocks
solve problems involving converting from hours to minutes; minutes to seconds; years to months; weeks to days.
- Solve problems involving units of time, explaining and recording how the problem was solved. For example: Raiza got into the pool at 2:26 pm. She swam until 3 o’clock. How long did she swim? They count on to find the difference between two given times, using a number line or time line where appropriate and use the 24-hour clock to measure time.
- The first clip in the series Great Primary Lesson Ideas from Teachers’ Media is entitled Magic Potions and it demonstrates a lovely activity for capacity. A Year 3 teacher has 'turned herself' into a witch to encourage her class to measure different volumes of coloured potions accurately, in order to make their own magic potion! Easily adaptable for Year 4. NB: Login (free) required.