| Programme of Study statement |
Activity |
|
|
| A |
B |
C |
D |
E |
F |
G |
| count up and down in tenths; recognise that tenths arise from dividing an object into 10 equal parts and in dividing one-digit numbers or quantities by 10 |
|
|
|
|
|
|
|
| recognise, find and write fractions of a discrete set of objects: unit fractions and non-unit fractions with small denominators |
|
|
|
|
|
|
|
| recognise and use fractions as numbers: unit fractions and non-unit fractions with small denominators |
|
|
|
|
|
|
|
| recognise and show, using diagrams, equivalent fractions with small denominators |
|
|
|
|
|
|
|
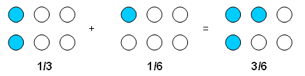
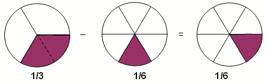
| add and subtract fractions with the same denominator within one whole (e.g. 5/7 + 1/7 = 6/7) |
|
|
|
|
|
|
|
| compare and order unit fractions, and fractions with the same denominators |
|
|
|
|
|
|
|
| solve problems that involve all of the above |
|
|
|
|
|
|
|
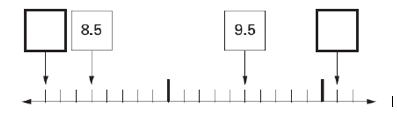
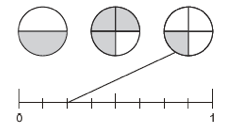
Activity A – visualising fractions along a line
- Use counting sticks and bead strings to help children visualise fractions.
If the bead string represents one whole, then each set of ten coloured beads could represent one tenth and each individual bead could represent one hundredth.


- Label the two ends of the bead string as 0 and 1. Give students tags to place each tenth on the bead string. You could use a 1-10 bead string instead of a 1-100 bead string.
- Join several bead strings together to create fraction lines that extend over one. For example, five bead strings allow fractional numbers from 0 to 5. Label simultaneously in mixed numbers (2 ½) and improper fractions (5/2).
- Ask the pupils to represent each tenth with a variety of manipulatives, for example, Numicon, Dienes (Big Base) and coins.
- Extend pupils’ understanding to include the equivalence of fractions, decimals and percentages. For example, ½ = 0.5 = 50% or 2 2/10 = 2.2 = 220%
Activity B
This practical activity develops an understanding of the part and the whole,
A series of lessons on finding fractions of amounts from Lesson 11, page 9 onwards based on an alternative, Hungarian approach, to teaching maths.
Activity C
An activity from New Zealand that involves using number rods to develop children’s understanding that fractions can extend beyond 1.
-
Children can make number lines for display around the classroom, that demonstrate counting in different fractional steps. For example counting in steps of ½ an apple, 1/4s of pizza, 1/10 of a £1 (steps of 10p)
-
Daily practice of counting forwards and backwards in 1/2s, 1/4s, 1/10s and 1/3s, including extending to below zero
Activity D – equivalent fractions
An activity based on Cuisenaire / number rods.
A ‘pelmanism’ style matching activity based on fractions.
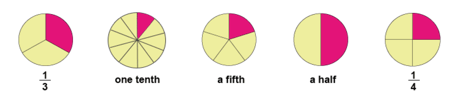
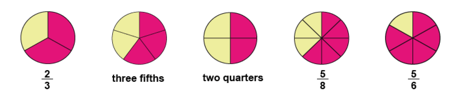
- Use equivalence circles, for example pizza or cake slices in a variety of activities for pupils to explore equivalence.

Activity E – adding fractions
A series of activities based on deepening students’ understanding of adding and subtracting fractions with the same denominator.
- Use a variety of representations, for example, number rods, paper strips and equivalence circles to model what happens when you add or subtract fractions with the same denominator. This will help children understand why the denominator doesn’t change.
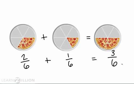
Activity F
(NB This resource was produced for the Primary National Strategy, which was formally discontinued in 2011. However, the resource has the potential to complement teaching in line with the new 2014 mathematics curriculum)
This ITP allows you to divide a green strip into a number of equal parts and colour the individual parts in yellow, clearly showing any comparison.
Use mini packets of smarties for children to find the fraction of each colour in a packet. This is useful for comparing fractions with the same denominator and for adding and subtracting fractions
More wonderful ‘Maths and Smarties’ ideas.
Activity G – solving problems
Use the ‘Thinking blocks on the maths playground’ website to model word problems involving fractions and to model adding and subtracting unit fractions. There are video demonstrations, guided problems and the ability to use the blocks to solve your own problems.
Assess and develop children’s understanding of equal sharing with this picnic problem.
Useful Resources
A list of models and images to support the development of children’s understanding of fractions. Includes ideas on how to use them in the classroom.
All the Overcoming Barriers materials from level 1 to level 5 linked to fractions, decimals and percentages contain useful assessment questions and a range of models and images.