The Five Big Ideas – Coherence

Dr Debbie Morgan, the NCETM’s Director for Primary, answers all our questions about coherence in this Q&A feature. Learn what coherent teaching means, how to develop this approach in your own school, and find out Debbie’s top three tips for teachers.

What do we mean by coherence and how does it fit into the Five Big Ideas in teaching for mastery?

In the dictionary, coherence is defined as a ‘systematic or logical connection or consistency’ and in the latest Ofsted report on maths it is described as a ‘forward-facing, base of mathematical knowledge rather than a collection of disconnected algorithms and tricks’.

There are two key elements here:

1. The order of the learning.
2. Making connections within the learning.

In terms of the Five Big Ideas in teaching for mastery, coherence strongly links to variation, where learning is built in small but connected steps. This happens within a lesson, across lessons, and across years. It's not about one task that will support children's learning, but considering the sequence of tasks and the links that are made over time. I often model a lesson when I work with schools, and teachers say, ‘that was great Debbie, I'm going to go and teach that tomorrow’, but I always urge them not to. We need to consider what comes before and have an eye on what is coming next – coherence is all about how the learning builds in ways that make sense to children.

• READ: The Five Big Ideas – Variation 

How should teachers apply the idea of coherence to their maths lessons?

Start at a point that is accessible to all pupils. Build the learning in small, connected steps to take children on a journey through a logical sequence, which is coherent and makes sense to them. 

Slow down where necessary to ensure that every child is with you. Constantly check: are they on the journey with you and is it making sense to them? This can be done through careful questioning, providing opportunities for focused talk, and listening into the focused talk between children. This is also where our adaptive teaching comes in; we slow down and take more time on things when children need more support.

• LISTEN: Podcast – Debbie Morgan discusses differentiation

It is crucial that the sequencing is coherent to you and other teachers in your school – if you can't make sense of it, then the children definitely won’t! Understand how it is linked to the learning that has gone before and have an eye on where it is going.

For example, we want children to know that when we compare two fractions that have the same numerator, we can generalise that ‘the larger the denominator, the smaller the fraction’ because there are more parts in the whole so each part must be smaller. But if we teach that in the first lesson, children will not make any sense of it – the important thing is the journey that gets them to that point.

Here is another example, from the Year 6 Professional Development materials. This focuses on developing understanding of how to find the area of a triangle:

It aims to teach pupils that the area of a triangle can be calculated by multiplying the base by the perpendicular height, and then dividing into two. We can't start a lesson with that because children wouldn't be able to make sense of it. They might try to remember it, but we want more than just remembering, we want them to really understand why.

Instead, the learning sequence starts with previous knowledge about the properties of triangles and the concept of area, and then we're able to build understanding in a coherent manner to be able to calculate the area of a triangle. There are lots of steps and sense making that needs to happen along the way. 

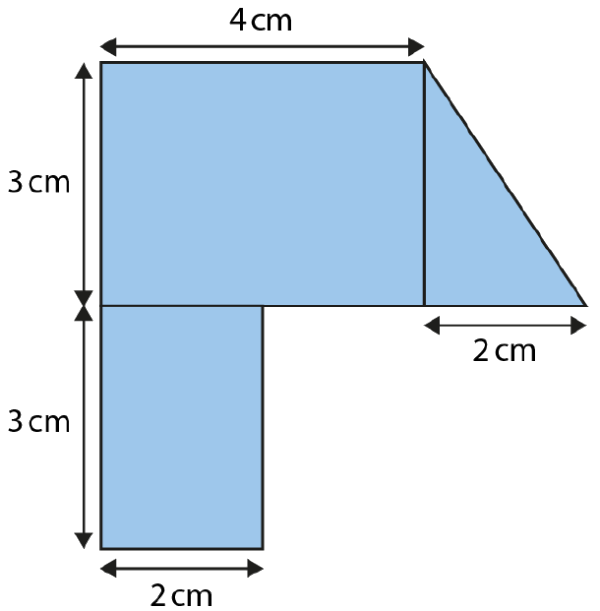
At the end of the unit, pupils get to this question where we see a composite unit of rectangles and a triangle:

This is quite a complex question, definitely not one we could have started with, but by this stage children are confident and have all the understanding they need about the concept of areas of triangles to tackle this with ease.

What is the potential positive impact of considering coherence?

Put simply, children make progress – that is a huge positive! Through ensuring we teach in a coherent way, we scaffold the learning to enable all pupils to understand and connect ideas together. 

Sometimes people think this way of teaching is only for the low prior attaining children, but it’s helpful for high prior attainers too. Sometimes it appears they understand because they can get the right answers, but there might be elements that are missing which don’t emerge for a long time. Maybe they might even get a top grade at GCSE, but then they start A level and suddenly things start to fall apart, because the firm foundations have not been built. We cannot risk this happening. It's not just about doing the maths; it's about gaining a deep understanding of the concept.

Consistency across the school is important. If all teachers are doing this and you have a coherent learning sequence across the school – not just within a unit, a term or one year group, but across the whole school – then it will be much easier for children to progress.

Coherence also keeps the class together, which makes teaching easier. Not because we're holding pupils back, but because everyone is going deep enough to build those firm foundations for later learning to be successful. The order of the teaching does matter and, if we can get that right, then learning will be far more successful. 

What teachers often experience is that some children find the learning becomes harder and harder over time and we want to turn the tide on that trend – with a coherent approach, maths should become easier and easier because we're building on previous learning.

This video is of a Year 3 lesson on number lines – note how the children go on a journey:

They started with number lines from 1 to 10 and then connected that to 1 to 100, then 1 to 1,000, so by the end of the lesson they are placing three-digit numbers, which is the requirement for Year 3. Building up to a thousand number line in coherent steps proves to children that those number lines behave in exactly the same way.

Is there only one journey or sequence that will work?

No, there are several ways that this can be done.

For example, there are two major structures in teaching addition. Aggregation – taking two quantities and putting them together to create a whole, and augmentation – increasing an existing quantity. So, do we start with aggregation or with augmentation? 

Well, it doesn't really matter! The important thing is that we teach both, otherwise children get a limited understanding of additive structures. We can then compare the two and make connections. However, for other concepts such as multiplication and division, I would argue that it makes sense to teach multiplication first. If children see multiplication as combining equal groups, we can build on that and see division as starting with a whole quantity and splitting it into equal groups. This shows that division is not a separate thing, but it's very much connected to multiplication.

What are some of the challenges that teachers might face?

One of the things that is often talked about is the curse of knowledge. The journey the teacher has planned might well make sense to them, because they know what is coming and they already understand this bit of maths, but they need to put themselves in the position of a pupil who is learning it for the first time.

It can be very tempting to miss out some steps but that is dangerous. Even though it might seem too easy or too obvious, for some children it might not be obvious, and no child will be harmed by it being easy. But, if we miss out steps, then we risk the learning becoming unsuccessful and leaving children behind. It is important to have detailed, small steps, that are connected – I can't emphasise that enough.

Teachers might have a sense that the pace is too slow. I would say that going into this level of detail will mean that the pace is quicker in the long-term, because you don’t need to go back and re-teach.

What are your three top tips for teachers who want to improve coherence in their lessons?

Use quality materials to support your subject knowledge. It requires a high-level of subject knowledge to generate those small steps so seek out materials that support you, such as the NCETM Professional Development or Curriculum Prioritisation materials.

Plan collaboratively. Talking through a sequence of learning with somebody else is invaluable. Even if you can’t do it all the time, it’s worth making time for collaboration when you can, as you will pick up transferable ideas that can be used when you are planning alone. Better still, get involved with your Maths Hub, which provides opportunities for teachers to collaboratively design lessons together.

• WATCH: Teachers engage collaborative planning

Don't overdo it. One thing I would warn against is making too many connections at once, as this can overload pupils. Ask the question: what is the core connection that needs to be made on the journey at this particular time? Choose the thing that will advance the learning towards where you are going and only once these are secure should you make other connections.

Summary

Coherence is more than just a sequence of great tasks. It's about putting those tasks in order and ensuring that they build and carry the learning forward. It’s about being explicit about mathematical connections and sense-making, so keep checking that children are making sense of every step, and that they are bringing all those ideas together to gain a clear understanding of the maths.

Did you enjoy this?

Read our previous Five Big Ideas features:

• Variation
• Representation and Structure.