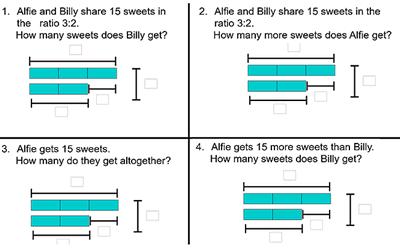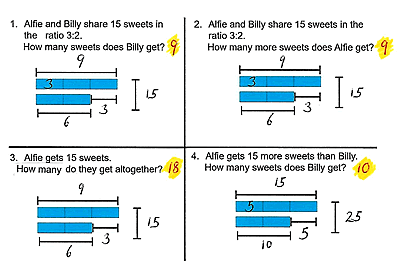How variation has changed my teaching

I’d been teaching maths for over ten years before I even heard the word ‘variation’ in relation to my job. Now, the word, and what lies behind it, is in my mind almost all the time. I consider it from the moment I conceive a lesson to the moment the students walk out of the door when the bell rings.

Every step of the way I’m weighing up what small changes I can make between examples I show on the board, or questions I pose to the class. I want my examples to provoke productive thinking. All the time, I want students to notice what’s the same and what’s different between two examples or questions, because that’s one route to deepened understanding.

My conversion began on an aeroplane. In September 2015, I flew to Shanghai with a group of secondary maths teachers as part of the Maths Hubs England–China exchange programme. On the flight I got my nose into a book we’d all been asked to read before the trip. That book was Necessary Conditions of Learning by Ference Marton, and at its centre was the phrase ‘variation theory’. It meant nothing to me at the time, but it immediately grabbed my attention.

It also helped me look for, and then notice, small but important details of the maths lessons I observed in Shanghai. Without reading the book I might have missed the beauty of the way these lessons had been constructed.

What I saw included:

• carefully crafted lessons that addressed one narrow concept in depth
• examples of the concept, along with common misconceptions
• practice with a purpose (intelligent practice).

When I came back, I started to try out some of these ideas in my own teaching. I talked to other teachers and I read more widely about variation theory. I won’t attempt to define variation theory here, because there are others far better qualified than me to do that. But I’ll explain what it means for me and my teaching. These are the things I now try to do more of:

• When I plan a lesson, I focus on one narrow concept in greater depth.
• When thinking of examples to show during a lesson, I think of standard and non-standard examples, and misconceptions.
• When thinking of what questions to pose, I ask myself what I want students to notice. This is when I decide what stays the same and what changes.

Here’s an example of one activity I have devised, which attempts to draw out some of the principles of variation theory.

I start by showing the students these four diagrams:

click image to enlarge

This activity was devised to address the common misconception of students just sharing the amount in the given ratio, regardless of the question. Every question has the same model, representing a 3:2 ratio-sharing, and also features the number 15. But, the role of the number 15 varies. It could be the total number of sweets (whole), the number of sweets Alfie or Billy has (a part), or the difference in the number of sweets that Alfie and Billy have (difference).

This way, I can be confident that the students’ attention will be drawn to what is different. If I changed the ratio and changed the ‘15’, students’ attention could be drawn to any of those things.

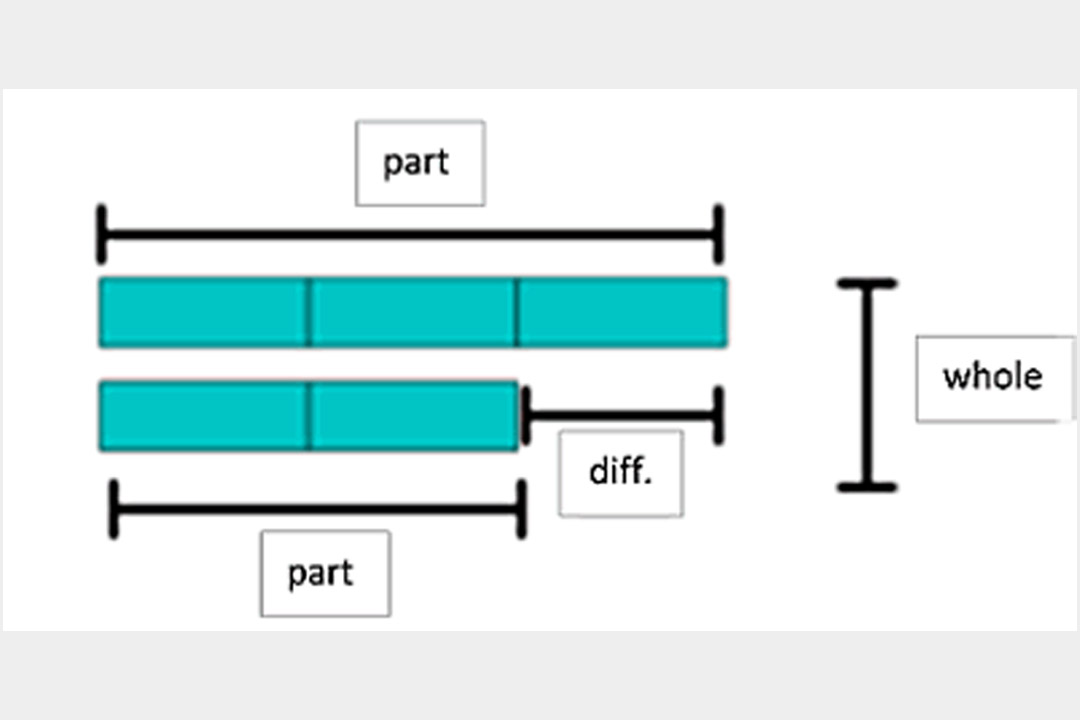
This diagram underlines the two parts, the difference, and the whole:

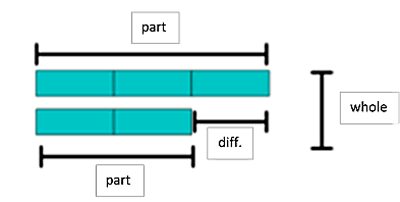
The aim of this exercise is to make students think about what is given in the question and what they are being asked to find.

This is how I take the class through the activity.

1. Explain that in all scenarios, Alfie and Billy share sweets in the ratio 3:2.

2. Show how the diagram represents this sharing ratio.

3. Point out that, in the top two cases, we know that they share 15 sweets between them, but in the bottom two cases we are not given that information. I leave the class, then, to work out what the 15 ‘means’ in the bottom two examples.

4. I ask them to annotate the diagrams, initially just putting the 15 where it belongs and a question mark in the position of the number being sought. I’m looking for students to produce something like this: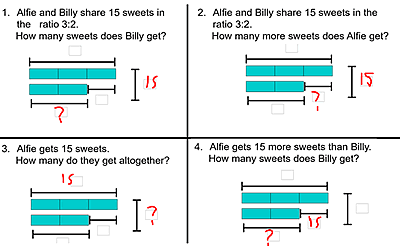


click image to enlarge

5. I model the language of part, whole and difference:

• • Q1 gives the whole and asks for a part.
  • Q2 gives the whole and asks for the difference.
  • Q3 gives a part and asks for the whole.
  • Q4 gives the difference and asks for a part.

6. I illustrate some common misconceptions reflected in incorrect answers (shown in red text on yellow background below):

click image to enlarge

7. I ask students to mark and correct the work and identify the misconceptions behind the incorrect answers.

8. I get students to write model solutions to the original questions, annotating part, whole or difference.

9. I follow up this activity by giving students a worksheet with the same models. In it, I ask them to write four different questions, keeping the ratio as 3:2 and using the 15 in one way or other. I start by asking what could be different. Typical responses would be “15 could be the number of sweets Billy gets and I could ask for the difference”.

10. I get students to check each other’s work and make sure each question is different.

A word of warning! The first time I tried this, imaginations ran wild. Students’ focus was on which two pop stars they were going to share sweets between, or trying to use really big numbers to make the questions harder. The next time I tried it I just used A and B and the ratio 3:2 and 15.

11. I add challenge by allowing students to change the 15. They must explain which numbers could work to give whole number/integer solutions.

This is just the start. From here I would keep changing just one thing at a time. For example, I would show a ratio of 5:2, which makes the difference have three equal parts. Next, I would move on to ratios in three parts and then on to GCSE-type questions where students create their own models.

The key thing for me is realising that if you only change the thing you want them to notice, they are more likely to notice it. Obvious, but so effective.

Jayne Webster, who teaches maths at Denbigh School in Milton Keynes, wrote this article in 2019. She is currently a Secondary Mastery Specialist and the Senior Leadership Link for Enigma Maths Hub.

If you want to find out more about variation theory, take a look at these resources:

• Enigma Maths Hub, where you can find examples of problems
• the NCETM’s explanation of variation theory and further reading
• themes and principles of mastery in secondary schools, from the NCETM.