Aligning curriculum and assessment reform with teaching for mastery in secondary maths (part 2)

In this two-part blog post with Carol Knights, the NCETM’s Director for Secondary, we suggest ways the curriculum and assessment of secondary maths could be improved. In part one, we explored the curriculum and its crucial role in shaping how students understand, enjoy and engage with maths.
In part two, we turn to assessment – an equally vital element in helping students succeed in maths and feel confident in their mathematical ability in an increasingly data-driven world.

There's also a further blog post on curriculum and assessment reform with Emma Bell, the NCETM’s Director for Post-16 GCSE and Functional Skills Qualifications (FSQ).

Part 2: Assessment

We know that too much focus on preparation for GCSE Mathematics assessment can have a significant, negative impact on how maths is taught in secondary schoolsⁱ.

In addition to curriculum adjustments, explored in part one of our blog post, restructuring GCSE Mathematics assessment has the potential to support deeper, more secure mathematical learning. 

The purpose of GCSE Mathematics

GCSE Mathematics should serve two key functions:

1. To assess whether students have the fundamental mathematical knowledge and skills everyone needs for life and work.
2. To assess whether students have developed the mathematical foundations needed for further study in STEM subjects and other disciplines which require quantitative analysis. 

Both functions are extremely important for young people, and society as a whole.

The current GCSE Mathematics structure means that neither of these functions are fulfilled well.

Problems with the current structure of GCSE Mathematics assessment

The nature of maths, as a subject where progression through the curriculum requires a deep and connected understanding (mastery) of what has gone before, means that lower attainers in maths are often unable to access questions that are accessible to higher attainers. It is for this reason that the current GCSE Mathematics has a tiered structure:

• Foundation tier maths assessment should enable students to demonstrate they have acquired the fundamental mathematical knowledge and skills required for life and work, and support further study in disciplines that require basic mathematical knowledge and skills. 
• Higher tier maths assessment should enable higher attaining students to demonstrate they have acquired the basic mathematical knowledge and skills required for life and work, and support further study in mathematics and other disciplines which require more sophisticated mathematical knowledge and skills. 

This structure is not working well: 

• Decisions about a student’s tier of entry are often made at the start of Year 10, or even earlier in some schools. This can be demotivating for those assigned to the foundation tier (around half the Year 11 cohort).
• Very low grade boundaries for the lower attaining students at each tier result in a significant proportion of the cohort having little opportunity to demonstrate the maths they know and can do.

The table below, showing GCSE Mathematics grade boundaries for the different awarding bodies for the June 2024 GCSE Mathematics exams, highlights the problem.

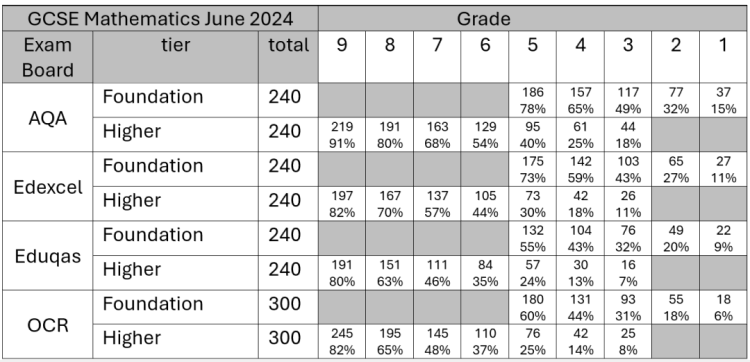In both tiers, students achieving the lower grades (1 and 2 in foundation tier and 3 and 4 in higher tier) are achieving very low marks.  In the higher tier, even those achieving a grade 7, a very good pass, may still be gaining fewer than half of the marks. 

This is:

• demoralising for the young people concerned, potentially putting them off mathematics
• unhelpful to employers and post-16 teachers because the lower grades in each tier do not indicate how well young people are prepared for the maths they will need in post-16 education or employment.

Furthermore, achieving a grade 4, or a ‘Level 2 pass’, is very high-stakes for students because those who do not achieve a grade 4 or above are severely disadvantaged in their future life and workⁱⁱ, and so must continue to study maths at Level 2 post-16ⁱⁱⁱ.

This means that the low grade thresholds for achieving a grade 4 on the higher tier (between 13% and 25% in 2024, depending on the awarding body), can encourage ‘gaming the system’ and ‘teaching to the test’, which damage students’ maths education. In 2023, the most recent year for which data is available, around 40,000 students achieved a grade 4 on the higher tier, meaning they are likely to ‘… have scored 20-33% of the marks to obtain that grade’.^iv

Many young people, and often their parents and teachers, view the purpose of secondary maths education as being to achieve a grade 4 or above in the GCSE Mathematics examination, rather than to acquire important knowledge and skills that will be invaluable to them in life, work and further study.

Reforming GCSE Mathematics assessment to enable all students to demonstrate their understanding of and ability to use fundamental mathematics would improve motivation and help ensure lower attaining students are better prepared for post-16 education and employment.

Our aim should be for young people to achieve a deep, connected understanding of maths, so that they are able to use it with confidence in their future life. 

A key problem with the current structure is that examination papers must cover such a wide range of attainment: 5 grades at foundation tier and 6 grades at higher tier, with grade 3 as a ‘safety net’^v. This makes it inevitable that those achieving the lower grades in each tier cannot access many marks.

Students’ maths outcomes could be improved through a reformed secondary school mathematics curriculum, as suggested in part one of our blog post, together with a different GCSE Mathematics structure to address problems caused by low grade boundaries. We have outlined two possible alternative structures below, presented not as solutions but to stimulate thinking. This is a complex challenge, and detailed development work and trialling must be undertaken before implementing changes.

Option A

Have two distinct maths GCSEs:

• ‘GCSE Mathematics 1’, with a maximum grade of 4, would focus on allowing all young people to demonstrate their knowledge and skills of the fundamental maths everyone needs for life and work, including application in context, so that the purpose and value of mastering this mathematics is clear. GCSE Mathematics 1 could be compulsory for all young people.
  The target boundary for grade 4 could be set quite high, for example at 75%, meaning that many students achieving less than a grade 4 would still be able to access a significant proportion of the marks, enabling them to demonstrate the maths they can do.
• ‘GCSE Mathematics 2’, which only assesses grades 5 - 9, would focus on equipping young people for further study in maths and other disciplines that require a more sophisticated mathematical knowledge and skills. This would be taken by around half the cohort, similar to the proportion of students taking the current higher tier GCSE Mathematics assessment.
  The target grade 5 boundary could be set at 50%. Students achieving a grade 5 would have a good opportunity to demonstrate what they can do, with plenty of marks available for higher grades to distinguish themselves.

All students would be required to take a GCSE Mathematics exam at the end of Year 11. Most would take both GCSE Mathematics 1 and 2 at the end of Year 11.

Option B

Keep the single GCSE Mathematics assessment, but structure it differently:

• Paper 1, focusing on grades 1, 2 and 3 only
• Paper 2, focusing on grades 3, 4 and 5 only
• Paper 3, focusing on grades 5, 6 and 7 only
• Paper 4 extension, focusing on grades 7, 8 and 9 only.

To achieve a GCSE Mathematics, students would need to take either:

• Papers 1 and 2, with the possibility of achieving up to a grade 5
• Papers 2 and 3, with the possibility of achieving up to a grade 7
• Papers 2, 3 and 4, with the possibility of achieving up to a grade 9.

Students who struggle with maths could take just Paper 1 at age 16, focusing on mastering fundamental skills before continuing post-16 to achieve their best grade by age 18.

With each paper covering only three grades, grade boundaries could be set so that the minimum grade for each paper requires 50% of the marks. This would allow all students to demonstrate their abilities on each paper, whilst leaving ample marks for higher achievers to stand out.

Conclusion

The current GCSE Mathematics structure does not work well and needs reform. A GCSE Mathematics structure is needed that:

• enables all students to demonstrate the maths they know and can do
• encourages deep learning of fundamental maths for all, to equip young people with the skills they will need for life and work
• enables appropriate stretch and challenge for higher attainers in maths.

The devil will be in the detail, but the possible alternative structures for GCSE Mathematics outlined above suggest that it would be possible to design an assessment structure that better meets the needs of students, employers and further education providers. 

Such reform would require detailed work, with proposed changes carefully trialled to avoid unintended, negative consequences. The Curriculum and Assessment Review offers an important opportunity to change GCSE Mathematics assessment in ways that can improve student learning and support better maths education outcomes for all young people.

ⁱCoordinating mathematical success: the mathematics subject report

ⁱⁱThe far-reaching consequences of failing to gain a grade 4-9 in English and Maths GCSEs

ⁱⁱⁱ16 to 19 funding: maths and English condition of funding

^ivGCSE Mathematics - charting grades, participation by age and tiering

^vGCSE Subject Level Conditions and Requirements for Mathematics