Meeting the needs of all without ability setting
Removing setting from maths teaching in a three-form entry primary school

Tom Collins is maths lead at St Joseph’s Catholic Primary School in Guildford, and one of the Primary Mastery Specialists being trained under the Maths Hubs Programme. He exudes enthusiasm about the effects that teaching for mastery is having on pupils across the attainment range. Impressed by his observations of Shanghai teachers in a local school, he has thought carefully about the practicalities of implementing teaching for mastery in his school. “We aren’t about ‘becoming Shanghai',” he says; “it’s about taking the elements of teaching for mastery that can be applied in our own schools, in our own classrooms, and implementing them, one considered, sure-footed step at a time.”
Teaching all-attainment classes
Tom felt that removing the setted structure in his three-form entry school was a strong initial step in encouraging teachers to try new methods to improve mathematical learning. “We had traditionally taught ability sets in Years 5 and 6 for many years, believing that the gap was so vast by this point we couldn't conceivably support and challenge children in mixed ability classes. However, consistently, attainment in English (where we continued to teach in mixed ability classes) was always better. As a result, we phased out maths ability sets in Year 5 last year (2014/15) and have brought the same year group into Year 6 without ability setting this year. It was an unpopular move with a handful of parents at first; however, we have been careful to ensure the most confident children are always challenged and engaged in class and so any resistance was short-lived.”
Teachers accustomed to working with ability sets often express concerns about whether it is possible to stretch the quickest learners in mixed-attainment classes. Encouragingly, Tom has found that high-attaining pupils are demonstrating a greater depth of understanding that he had not always seen previously and finding maths lessons more enjoyable. “Previously my high-attaining Year 6 pupils would be siphoned off to tackle Level 6 material and whilst they are able to answer the Level 6 questions at a procedural level, they often do not recognise the concepts and connections in what they are doing. Now I see Year 6 high-attainers enjoying maths more as they really unpick the concepts.”
So how is Tom achieving this depth with high-attaining children, whilst scaffolding learning for the lower attainers?
Pair-talk
Notably, Tom uses pair-talk effectively and frequently, interspersed with individual pupils explaining their understanding to the class. During pair-talk episodes, Tom minimises his intervention, viewing this as a time for him to listen and learn about their depth of understanding, only intervening if he hears a misconception that needs to be addressed to avoid it being reinforced.
Tom arranges his desks in rows, with the pupils paired up, and those children that most often need help in seats that the teacher can physically get to most easily. “The pairings themselves are only selected for one reason [not perceived ability] – I ask myself, ‘Who will this child work alongside in a focused, supportive and collaborative manner?’” Pairings change every half term.
Importance of questioning style
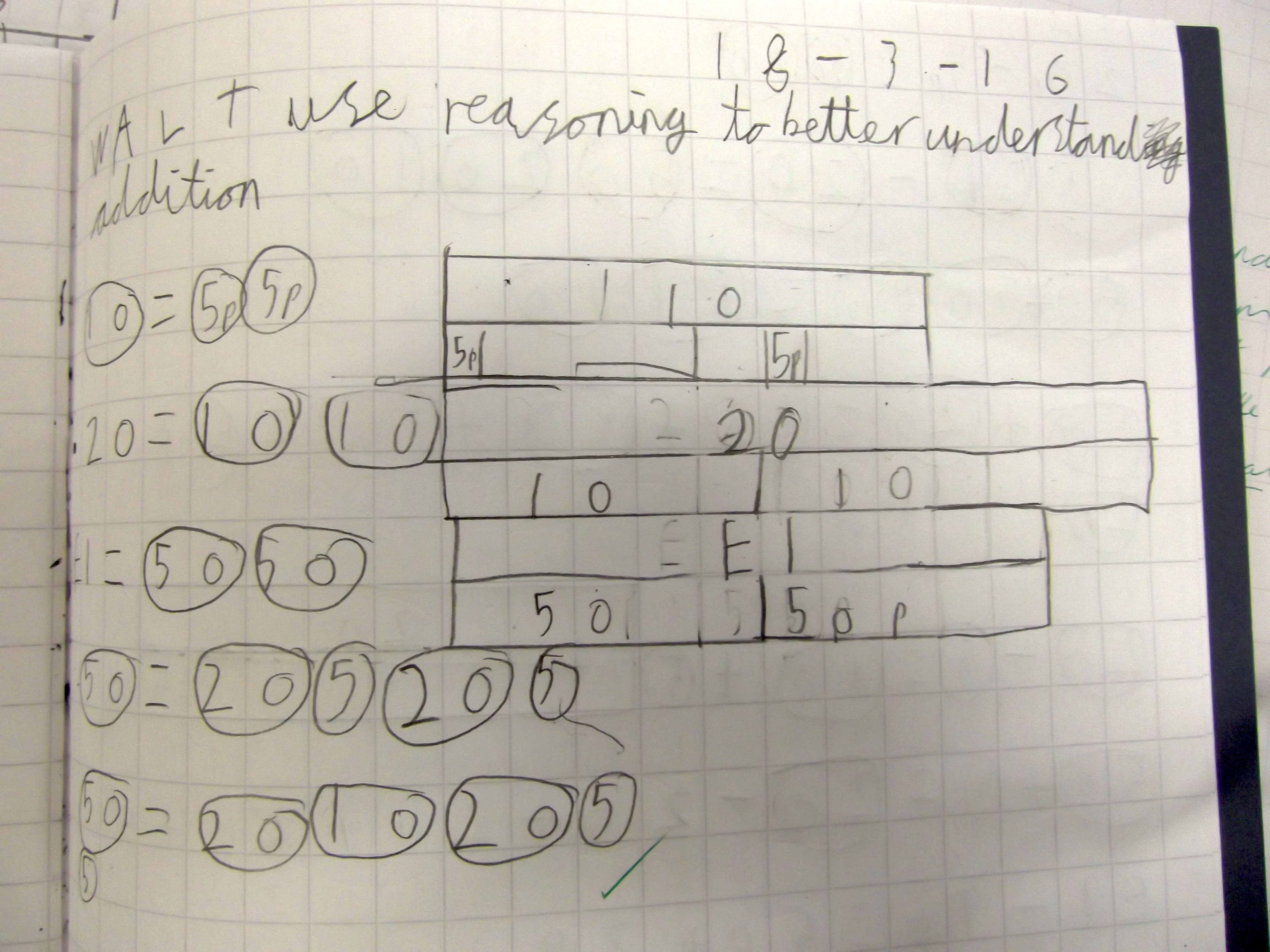
Continual encouragement to verbalise understanding to the rest of the class appears to be deepening meaning for all children. Children that have grasped the concept give deeper, more precise explanations. In a Year 3 lesson – forming additive equations with coins – some children were able to confidently explain proportional errors in bar models such as the one below, using precise language and proportional reasoning.
Other children are encouraged by Tom’s persistent, supportive and delving questioning style. Local teachers observing Tom’s lesson commented on how long he was prepared to wait patiently for a child to get to an answer, helping along the way, without giving up or moving on. Tom explains that he is attempting to overcome the familiar phenomenon of children ‘freezing up’ when put on the spot. He has observed that it is too easy for such children to say nothing and learn that the teacher will eventually provide the answer, or stop asking them. He makes it clear that he expects all to contribute.
Tom recognises two types of question in his teaching – questions to help probe and deepen understanding of new concepts and questions to assess children’s understanding of prior concepts. “I aim the first type of question at children I think can offer some helpful, insightful observations of a new concept (often based on what I've overheard during paired discussion beforehand) and I aim the second type of question at children who, based on my formative assessment, are likely to need to revisit a concept in order to secure new learning.” He tries particularly hard to ask questions that expose misconceptions and address them head on.
Carefully crafted lessons
Another tactic Tom uses, to ensure stretch for high attainers and scaffolding for others, is to very carefully craft his lessons, thinking precisely about every example he uses and every question set for pupils. This ensures slow but steady progression, by varying just one component of the questions at a time. Pupil work time is regularly punctuated by teacher-led discussion and examples, so Tom frequently ‘reels the kite back in’ after letting children run with it in their own work. This technique was evident in the final exercise (below) that Tom set for the Year 3 lesson, allowing children to reason that the final equation wasn’t possible ('letting the kite out'). He then demonstrated that an = sign in the second box, as well as the necessary + and – signs, could make the equation true ('reeling the kite back in').
This task was set in a Year 3 lesson on forming additive equations. Tom asked the children to insert mathematical symbols to make the equations true.
| Lesson resources for a 3-lesson unit forming additive equations using coins |
|---|
| 1. Additive Fluency [Pupil worksheet (Word) | Smartboard slides] |
| 2. Additive Reasoning [Pupil worksheet (Word) | Smartboard slides] |
| 3. Additive Problems [Pupil worksheet (Word) | Smartboard slides] |
In order to open the Smart files, you will need a copy of Smart software. If you do not have Smart software you can use the SmartTech website to open the Smart files.
This case study was first published in 2016.